◐
compsci compilers algorithms nlp javascript

Parsing Regex with Recursive Descent

Languages, Grammars, and Parsing

In computing, we use formal languages - programming languages, query languages, markup languages, protocols, config formats, etc. Using them, we define what we want the computer to do.

Formal grammars, on the other hand, are used to define the languages themselves. For every formal language, we have a corresponding grammar (usually context-free) that defines its structure.

Given a string and a grammar, parsing answers two questions:

The structure of the string relative to the grammar is denoted using a parse tree. If we can build a parse tree then the string is correct according to the grammar.

In this article, we’ll define a basic regular expression language using a formal grammar and learn how to parse its strings in linear time using the recursive descent method. We’ll use the BNF notation for the grammars.

Example Grammar #1

Let’s define the following grammar:

<S> ::= 'a'<A>'e'
<A> ::= 'b'<A>'d' | 'c'

\(S, A\) are called nonterminals, \(a,b,c,d,e\) are the terminal symbols. \(S\) is the start symbol (axiom) of the grammar and above we have depicted the two production rules. This grammar describes strings that start with an “a”, end with an “e”, have a “c” in the middle which is surrounded by an equal number of “b”’s to its left and “d”’s to its right. Some of the strings that belong to the language of the grammar are “ace”, “abcde”, “abbbcddde”, etc. We can examine the structure of these strings by building the corresponding parse trees.

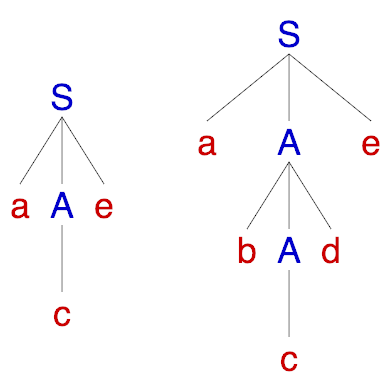
Given a valid parse tree, we reconstruct the input string by traversing it depth-first and concatenating the labels of the leaf nodes.

Recursive Descent Parsing

Recursive descent parsers belong to the class of top-down parsers, meaning, they construct the parse tree starting from the start symbol of the grammar (the root of the tree) and make their way towards the leaves. The rules in the grammar are applied from left to right. They are fascinating due to their simplicity, elegance and can run in linear time for some types of grammars.
This is a hands-on article, where we’ll define a formal grammar for regular expressions and build a corresponding parser. We’ll use JavaScript as a language of choice, but the concepts are universal and can be transferred to any other language.

A recursive descent parser is simply a set of functions for each nonterminal in the grammar. We begin parsing by executing the function corresponding to the axiom and terminate successfully if the whole input string has been processed. Suppose we have the following rule:

\[ A \to X_0 X_1 \dots X_n \]

where \( X_i \) is either a terminal or a nonterminal. Pseudocode for the corresponding function would look like this:

function A() {
    foreach Xi in X0...Xn
        if Xi is a nonterminal
            call the function for Xi()
        else if Xi is a terminal and Xi == current input symbol
            advance the to next input symbol
        else
            handle an errror (backtrack or throw)
}

Source: Compilers: Principles, Techniques, and Tools (The Dragon Book), Chapter 4 Syntax Analysis

A simple recognizer for grammar #1 using recursive descent can be found here.

Parsing Regular Expressions

We start by defining the grammar of our regular expressions. We are going to support the base operations such as concatenation, union (|), zero-or-more (*), one-or-more (+), zero-or-one (?), and grouping (()). We’ll also allow users to use metacharacters (*,+,?) as ordinary symbols through escaping (\).

<expr> ::= <term>
    | <term>'|'<expr>
<term> ::= <factor> 
    | <factor><term>
<factor> ::= <atom>
    | <atom><meta-char>
<atom> ::= <char>
    | '('<expr>')'
<char> ::= <any-char-except-meta>
    | '\'<any-char>
<meta-char> ::= '?' | '*' | '+'

We can see that the operator precedence is encoded in the grammar as the lower priority operations (e.g. |) are situated closer to the root of the parse tree whereas the higher priority ones (?,*,+) are closer to the leaves. We depict concatenation through the <term> ::= <factor><term> production rule.

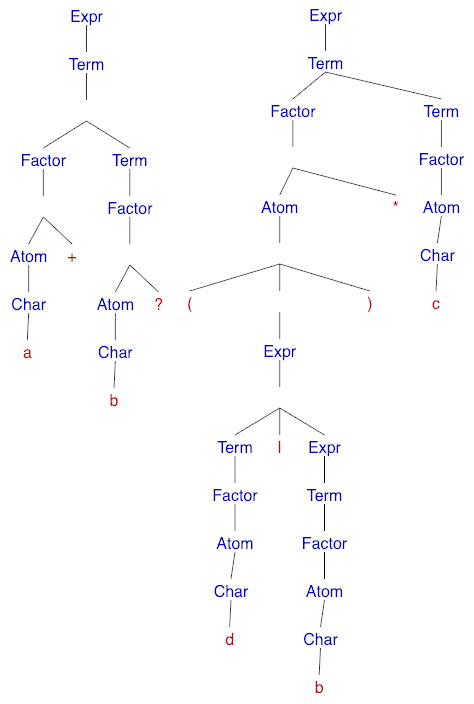
Above are the parse trees for the strings a+b? and (a|b)*c respectively.

Let’s introduce some auxiliary functions before implementing the parsing procedure. First, we define the constructor function for the tree node.

1
2
3
4

function TreeNode(label, children) {
    this.label = label;
    this.children = children || [];
}

A tree node is an object holding a label (string) and an array with references to the child nodes. We continue by declaring some auxiliary variables and functions.

 6
 7
 8
 9
10
11

let pattern = '';
let pos = 0;

const peek = () => pattern[pos];
const hasMoreChars = () => pos < pattern.length;
const isMetaChar = ch => ch === '*' || ch === '+' || ch === '?';

peek() returns the current symbol in the input string, hasMoreChars() checks if we have reached the end of the input, and isMetaChar(ch) checks if we see a symbol that serves as a unary operator.

13
14
15
16
17
18
19
20
21
22
23
24

function match(ch) {
    if (peek() !== ch)
        throw new Error(`Unexpected symbol ${ch}`);
    pos++;
}

function next() {
    let ch = peek();
    match(ch);

    return ch;
}

match(ch) matches a character with the one we’re currently at and moves the position to the next input symbol, next() returns the current input symbol, and moves forward with one position.

Now we are ready to implement the functions for each nonterminal in the grammar. These functions have the same signature - they take no arguments and return an object of type TreeNode. We start with the axiom.

<expr> ::= <term> 
    | <term>'|'<expr>

26
27
28
29
30
31
32
33
34
35
36

function expr() {
    const trm = term();

    if (hasMoreChars() && peek() === '|') {
        match('|');
        const exp = expr();
        return new TreeNode('Expr', [trm, new TreeNode('|'), exp]);
    }

    return new TreeNode('Expr', [trm]);
}

Our code directly follows the derivations for expr. We continue with the term and factor.

<term> ::= <factor> 
    | <factor><term>
<factor> ::= <atom>
    | <atom><meta-char>

38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

function term() {
    const factr = factor();

    if (hasMoreChars() && peek() !== ')' && peek() !== '|') {
        const trm = term();
        return new TreeNode('Term', [factr, trm]);
    }

    return new TreeNode('Term', [factr]);
}

function factor() {
    const atm = atom();

    if (hasMoreChars() && isMetaChar(peek())) {
        const meta = next();
        return new TreeNode('Factor', [atm, new TreeNode(meta)]);
    }

    return new TreeNode('Factor', [atm]);
}

For term() we need to perform an additional check (line 41) of the next input symbol so we can expand the correct derivation. factor() similar to expr().

<atom> ::= <char>
    | '('<expr>')'
<char> ::= <any-char-except-meta>
    | '\'<any-char>

60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

function atom() {
    if (peek() === '(') {
        match('(');
        const exp = expr();
        match(')');

        return new TreeNode('Atom', 
            [new TreeNode('('), exp, new TreeNode(')')]);
    }
    
    const ch = char();
    return new TreeNode('Atom', [ch]);
}

function char() {
    if (isMetaChar(peek()))
        throw new Error(`Unexpected meta char ${peek()}`);

    if (peek() === '\\') {
        match('\\');
        return new TreeNode('Char', 
            [new TreeNode('\\'), new TreeNode(next())]);
    }

    return new TreeNode('Char', [new TreeNode(next())]);
}

The functions for the last two nonterminals <atom> and <char> follow the same pattern.

87
88
89
90
91
92

function toParseTree(regex) {
    pattern = regex;
    pos = 0;

    return expr();
}

Now we’re ready to complete the algorithm. We assign the new input string to the variable pattern (88), reset the input position (89), and call the function for the start symbol of the grammar (91) which is going to return the complete parse tree if the input string is correctly defined.

Regex to NFA using Recursive Descent

We can use the resulting parse tree to compile a nondeterministic finite automaton (NFA) using a simple recursive depth-first traversal. The structure is convenient as it naturally encodes the operator’s precedence.

The relationship between regular expressions and finite automata is discussed here, however, the article presents a different approach to parsing. You can also check out the complete adaptation of this recursive descent parser for NFA compilation:

Note that the procedure can be further simplified by constructing the NFA “on-the-fly” instead of first building a parse tree. For this, we need to adapt the parser’s functions for each nonterminal to return an NFA instead of TreeNode and perform the operations during the parsing which is practically a depth-first traversal by itself. You can check out the implementation of this approach, which also supports an extended regex syntax, here.

Conclusion

In this article, we briefly defined the concepts of formal grammars, parsing, and we’ve learned how recursive descent parsers generally operate. Then we specified our regex syntax using a context-free grammar and implemented a recursive descent parser based on its production rules. In the end, we’ve mentioned how this algorithm can be utilized for an efficient regex-to-NFA compilation procedure. It is also easy to see how our regular expression grammar and its parser can be extended to support additional syntactic constructs such as character classes, counts, etc.

References and Further Reading

comments powered by Disqus