|  Edit
compsci compilers nlp javascript

Translation using Syntactic Rules

Often, when we build applications we have to deal with some kind of a non-trivial input or come up with a standardized way of passing information between the components of a system. In cases like this, a rudimentary approach like using regular expressions, combined with control flow statements can quickly turn out messy, error-prone and leave little to no room for extension.

In this article, we’ll explore a formalism, widely used for describing computer languages, namely the Context-Free Grammars. We’ll learn how to define the syntax of a language using a grammar, parse strings of this language and generate the corresponding output - be it another string, or an in-memory data structure.
For the hands-on part, we’ll use ANTLR (ANother Tool for Language Recognition) to implement a CSV parser thus seeing how an abstract formalism can be turned into code.

Definition

Let’s take a look at ECMAScript’s specification of an if-statement:

IfStatement: 
    if ( Expression ) Statement else Statement
    if ( Expression ) Statement

The : means “can have the form” and such a rule is called a production. Productions consist of two types of lexical elements, namely terminals and nonterminals. In this case:

Formally

A context-free grammar \( \langle \Sigma, N, S, P \rangle \) consists of four components:

Grammar Notation

We write grammars by listing their production rules with the start symbol listed first. There are several ways to describe a grammar but for the remainder of this article, we’ll use ANTLR’s EBNF-style format.

start: expr;
expr: expr '+' DIGIT;
expr: expr '-' DIGIT;
expr: DIGIT;

DIGIT: '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9';

We can also group the bodies of the expr productions:

expr: expr '+' DIGIT | expr '-' DIGIT | DIGIT;

The terminals of the grammar are +,-,0,1,2,3,4,5,6,7,8,9, the nonterminals are start, expr and DIGIT where start is the start nonterminal.

We can also define our DIGIT lexer rule (token) using a regular expression:

DIGIT: [0-9];

You might be wondering why expr and DIGIT nonterminals are denoted differently. Although both are on the left-hand side of some productions, they represent different types of rules - namely lexer rules and parser rules (more on that in the next section). ANTLR imposes the convention that lexer rules start with an uppercase letter and parser rules with a lowercase letter.
Lexer rules contain only either literals (along with the use of EBNF symbols; literals can be both single characters and longer strings) or references to other lexer rules. Parser rules may reference parser and lexer rules as they wish and even include literals, but never only literals.

Derivations

The way we derive a string by a given grammar is by beginning with the start symbol’s production and replacing each of the nonterminals in its body with a corresponding production. We say that the language of grammar is the set of all strings that can be derived from its start symbol.

Lexical Analysis (Tokenization)

A lexer reads an input character stream and divides it into tokens, using the patterns that we specify (see DIGIT above), and generates a token stream as an output. It can also discard or flag some tokens like whitespaces and comments so that they’re ignored during parsing.

Let’s extend our token grammar so it includes integers and floating-point numbers.

// Parser rules
start: expr;
expr: expr '+' NUMBER
    | expr '-' NUMBER
    | NUMBER;

// Lexer rules
NUMBER: INT | FLOAT;
INT: DIGIT+;             // match one or more digits
FLOAT: DIGIT+ '.' DIGIT* // match 1.314, 5., 0.2 etc.
     | '.' DIGIT+;       // match .2, .3248 etc.
DIGIT: [0-9];

Given this grammar and the string “5+1”, the tokenizer will generate the following output:

[@0,0:0='5',<NUMBER>,1:0]
[@1,1:1='+',<'+'>,1:1]
[@2,2:2='1',<NUMBER>,1:2]
[@3,3:2='<EOF>',<EOF>,1:3]

So we have the value of each token, its type and its position in the input.

Parse Trees

The parser’s job is to figure out the relationship between the tokens. A parse tree shows how the start symbol of a grammar derives a particular string. It has the following properties:

“5+1” has the following parse tree:

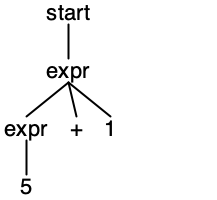
The leaves of the tree from left to right yield the string. Finding the tree for a given sequence of tokens is called parsing. Let’s see another example. The parse tree of “15+1.4-.2”:

We can generate “15+1.4-.2” by applying the production rules in the following order:

start
expr
expr - NUMBER
expr + NUMER - NUMBER
NUMBER + NUMBER - NUMBER
INT + NUMBER - NUMBER
15 + NUMBER - NUMBER
15 + FLOAT - NUMBER
15 + 1.4 - NUMBER
15 + 1.4 - FLOAT
15 + 1.4 - .2

Note: The expression grammars can get tricky as we have to deal with the operator precedence and associativity. As the initial example, I wanted to keep it as simple as possible, hence we have only addition and subtraction.
Grammars can also be ambiguous - that is we can have more than one parse tree for a given input. We won’t cover the various grammar types and parsing algorithms in this article, but I’ve provided some resources on the topic in the references below.

Parsing JSON

Let’s see another example. The following grammar denotes a proper subset of the JSON language.

grammar JSON;
// Parser rules
json: object 
    | array 
    |   // empty string is a valid json
    ;

object: '{' pair (',' pair)* '}' // one or more key-value pairs
      | '{' '}';  // empty object

pair: STRING ':' value;

array: '[' value (',' value)* ']' 
     | '[' ']'; // empty array

value: STRING | NUMBER | object | array | 'true' | 'false' | 'null';

// Lexer rules (simplified for brevity)
STRING: '"' [a-zA-Z0-9]+ '"';
NUMBER: [0-9]+;
WS: [ \t\n\r]+ -> skip; // discard tabs, whitespaces and newlines

Consider the following JSON:

{
    "key": "a1b2c3",
    "values": [1, 34, 10],
    "meta": {
        "readonly": false
    }
}

It would result in the following parse tree:

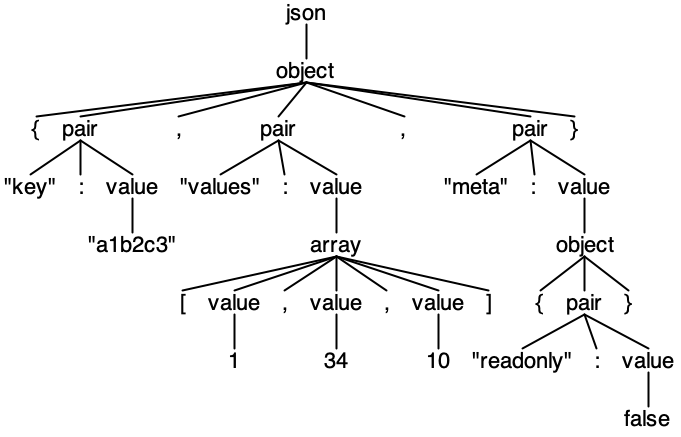
Generating a parse tree is a form of validation as well. If a parse tree cannot be generated from a given input - the input is invalid.

Syntax-directed translation

The syntax-directed translation is a compiler implementation technique where the translation is completely driven by the parser. In other words, the parse tree is used to perform the semantic analysis and the translation of the source. Once we’ve generated the parse tree, we have to visit each node and perform a specific action (think of it as a piece of code to be executed). As each node in a parse tree corresponds to a grammar rule, we can say that the action, attached to this rule carries its semantics. Keep in mind:

So far we’ve learned how to describe a structure of a language. Now is time to define its semantics.

Let’s go back to the arithmetic expression example and see how to calculate a result by performing a depth-first traversal of the parse tree. Consider the following input “5+3-1”:

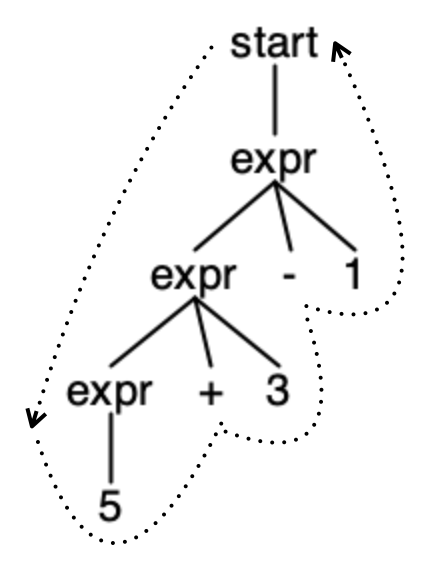
Knowing that the phrase structure is specified by a set of rules:

So in our tree walk, according to the grammar, we can either be in a node of type start, expr or in a leaf node which can represent the NUMBER, '+' or '-' tokens. The calculation procedure might look like this:

function visit(node) {
    if (node.isTerminal) {
        // Action "attached" to a terminal node
        return node.type === TokenTypes.NUMBER 
            ? parseFloat(node.getText()) 
            : node.getText();
    }
    // Action "attached" to a 'expr'/'start' node
    if (node.children.length === 3) {
        const left = visit(node.getChild(0));
        const op = visit(node.getChild(1));
        const right = visit(node.getChild(2));

        return op === '+' ? (left + right) : (left - right);
    }

    return visit(node.getChild(0));
}
visit(root); // '5+3-1' => 7

So calling visit(root) is going to return the result of the evaluation. An expr subtree has the following semantics - it can either have a single child which subtree evaluates to a number or three child nodes where the first and the third evaluate to a number and the second is an operator symbol. Depending on the operator, the node’s value is calculated.

Another example would be to convert the expression which is in infix notation into postfix notation.

function visit(node) {
    if (node.isTerminal) {
        return node.getText();
    } 
    if (node.children.length === 3) {
        const left = visit(node.getChild(0));
        const op = visit(node.getChild(1));
        const right = visit(node.getChild(2));

        return op + ' ' + left + ' ' + right;
    }

    return visit(node.getChild(0));
}
visit(root); // '5+3-1' => '5 3 + 1 -'

We would take the same approach if we are to implement a JSON to XML converter, or JSON to an in-memory data structure for example. This is also a very rudimentary and impractical way to attach actions to rules. In the next section, we’ll see a cleaner approach.

Hands-On: Parsing CSV

Everything so far was more or less abstract. Now is time to go through a real-world example and put what we’ve learned to practice. We’re going to implement a program that translates a CSV string to JSON. To generate our parser, we’re going to use ANTLR. Provided a grammar, ANTLR can emit the parser code in several languages (Java, C#, JavaScript and others). Check this guide for the installation details. We’re going to generate our parser in JavaScript.

We can split our task into two subtasks:

  1. Parsing - given a context-free grammar and a string, generate a parse tree.
  2. Translation - given a parse tree, generate an output.

Parser generation with ANTLR

Let’s define our CSV grammar in CSV.g4:

grammar CSV;

csvFile: hdr row+ ;
hdr : row ;
row : field (',' field)* '\r'? '\n' ;
field
    : TEXT
    | STRING
    |   // empty string
    ;

TEXT   : ~[,\n\r"]+ ;
STRING : '"' ('""'|~'"')* '"' ; // quote-quote is an escaped quote

source: grammars-v4 on GitHub

Let’s also create employees.csv.

EmployeeNumber, Name, Location, BirthDate
12420, John Smith, USA, 1988/04/29

We can now proceed to visualize the parse tree. Running

antlr CSV.g4
javac ./CSV*.java
grun CSV csvFile -gui -tokens ./employees.csv

would result in

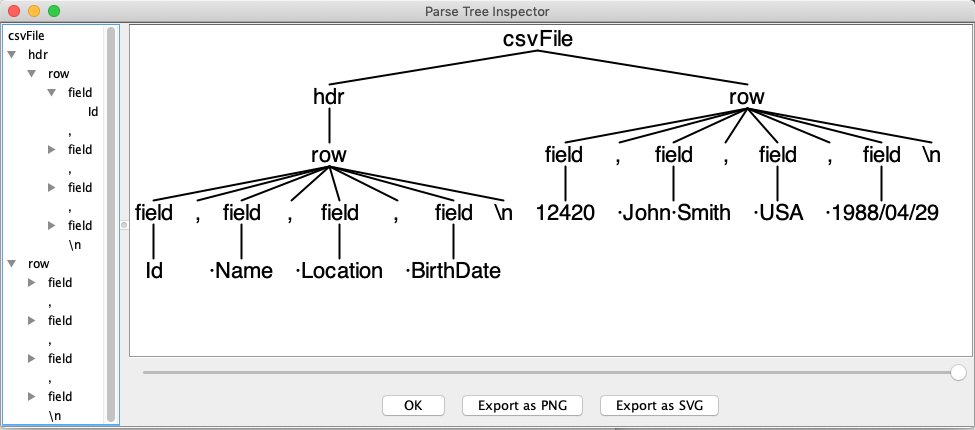
This is a useful tool for debugging our grammars, but now we’ll see how to programmatically construct and access the parse tree.
First we need to install the JavaScript target for ANTLR4.

npm i antlr4

Generate the parser, this time in JavaScript:

antlr CSV.g4 -Dlanguage=JavaScript -visitor -o lang/

ANTLR has generated a bunch of files for us.

ls lang
CSV.interp      CSVLexer.interp CSVLexer.tokens CSVParser.js
CSV.tokens      CSVLexer.js     CSVListener.js  CSVVisitor.js

We can see that we now have the lexer and parser source files. ANTLR has also generated two other files - CSVVisitor.js and CSVListener.js which we’ll cover in the next section as they are related to the translation phase.

We have a lexer and a parser. Now it’s time to generate the parse tree. Create main.js.

const antlr = require('antlr4');
const CsvLexer = require('./lang/CSVLexer').CSVLexer;
const CsvParser = require('./lang/CSVParser').CSVParser;
const CsvVisitor = require('./lang/CSVVisitor').CSVVisitor;

const input = `REVIEW_DATE, AUTHOR, ISBN, DISCOUNTED_PRICE
1985/01/21, Douglas Adams, 0345391802, 5.95
1990/01/12, Douglas Hofstadter, 0465026567, 9.95
`;
const chars = new antlr.InputStream(input);
const lexer = new CsvLexer(chars);
const tokens = new antlr.CommonTokenStream(lexer);
const parser = new CsvParser(tokens);
const tree = parser.csvFile(); // parse from the start rule (the axiom)

We’ve generated a parse tree, it’s time to go ahead with the translation.

Translation

ANTLR also generates a “parse tree walker” interface for us. That means we can easily hook into events during the parse tree traversal. For our translator, we’re going to use the visitor mechanism which is an implementation of the Visitor pattern. In ANTLR, the visitors and listeners are both used for traversing the tree but they are slightly different (more on that here).

Let’s take a look at the generated CSVVisitor.js:

// Generated from CSV.g4 by ANTLR 4.7.2
// jshint ignore: start
var antlr4 = require('antlr4/index');

// This class defines a complete generic visitor for a parse tree produced by CSVParser.
function CSVVisitor() {
	antlr4.tree.ParseTreeVisitor.call(this);
	return this;
}

CSVVisitor.prototype = Object.create(antlr4.tree.ParseTreeVisitor.prototype);
CSVVisitor.prototype.constructor = CSVVisitor;

// Visit a parse tree produced by CSVParser#csvFile.
CSVVisitor.prototype.visitCsvFile = function(ctx) {
  return this.visitChildren(ctx);
};
// Visit a parse tree produced by CSVParser#hdr.
CSVVisitor.prototype.visitHdr = function(ctx) {
  return this.visitChildren(ctx);
};
// Visit a parse tree produced by CSVParser#row.
CSVVisitor.prototype.visitRow = function(ctx) {
  return this.visitChildren(ctx);
};
// Visit a parse tree produced by CSVParser#field.
CSVVisitor.prototype.visitField = function(ctx) {
  return this.visitChildren(ctx);
};

You can see that these function names correspond to the nonterminals in the grammar, ctx is the context of the current tree node. We can hook into and implement the semantics of each rule by extending this class. Think of these functions as augmentations to the grammar. They represent the actions we specify for our rules.

In CSV we have two types of rows - a row with values and a header row. Each row contains fields. So when building our translator, we have to handle the special case when a row node descends from a header (hdr) node (see the parse tree above).

class CsvToJsonConverter extends CsvVisitor {
    constructor() {
        super();
        this.header = []; // holds the header values
        this.currentRowValues = []; // holds the values of the current row
        this.output = [];
    }
    
    // The axiom's action is going to be invoked first.
    visitCsvFile(ctx) { 
        this.visitChildren(ctx);
        return this.output;
    }
    
    visitHdr(ctx) {
        this.visitChildren(ctx);
        // After traversing the 'hdr' subtree we store the values
        this.header = this.currentRowValues;
    }

    visitRow(ctx) {
        // Clear values added from the previous row node
        this.currentRowValues = [];
        // Traverse the subtree and collect the field values
        this.visitChildren(ctx);
        
        // Construct an object from a row in case is's not a header row
        if (ctx.parentCtx.ruleIndex !== CsvParser.RULE_hdr) {
            const item = {};
            this.currentRowValues.forEach((val, index) => {
                /* The header row is already visited because 
                   it is always the lefmost row node in the tree */
                const key = this.header[index];
                return item[key] = val;
            });
            this.output.push(item);
        }
    }

    visitField(ctx) {
        // When we visit a 'field' node, we simply store its text
        this.currentRowValues.push(ctx.getText().trim());
    }
}

Now we’ve specified how to “walk the tree” using our custom visitor.

const result = tree.accept(new CsvToJsonConverter());

is going to produce:

[ { REVIEW_DATE: '1985/01/21',
    AUTHOR: 'Douglas Adams',
    ISBN: '0345391802',
    DISCOUNTED_PRICE: '5.95' },
  { REVIEW_DATE: '1990/01/12',
    AUTHOR: 'Douglas Hofstadter',
    ISBN: '0465026567',
    DISCOUNTED_PRICE: '9.95' } ]

Parsing Regular Expressions

Another example is using syntax-directed translation for compiling regular expressions to finite automata. The article shows a stack-based approach, but we can also perform the compilation by writing a grammar and constructing a parse tree. A grammar that replicates the regex syntax as shown in the article would be:

grammar Regex;

start: expr;
expr: 
    '('expr')'
    | expr'*'      // closure
    | expr'.'expr  // concatenation
    | expr'|'expr  // union (or)
    | SYMBOL;

SYMBOL: [a-zA-Z0-9];

The operator precedence is specified by ordering the expr productions from the highest (top) to the lowest (bottom). Here’s the parse tree of “(a|b)*.c”:

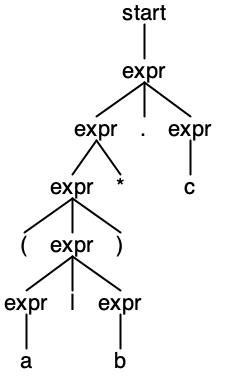
You can check out the compilation procedure here, however, for better understanding I recommend reading the regex article first.

Conclusion

In this article, we’ve learned an approach for formal language recognition and translation. We’ve introduced the context-free grammars and learned how to describe a language syntax using a grammar. Then we saw how to denote the structure of a string using a parse tree and work with this tree to derive the desired output. We also learned how to use ANTLR to generate a parser for a language and use its API to define its semantics.

The syntax-directed translation is not a new concept and has many practical applications. You can use the approach for processing query languages, protocols, connection strings, configuration files and all kinds of domain-specific and general-purpose languages. You can also build a custom language that suits your application’s domain, format code, inject code or check style. All you need is to know how to write grammars and write them well (see the references for more on the topic).

References & Further Reading

  1. Aho, Lam, Sethi, Ullmann (2007) Compilers: Principles, Techniques, and Tools (The Dragon Book) - Chapter 2: A Simple Syntax-Directed Translator, Chapter 4: Syntax Analysis
  2. Terence Parr (2012) The Definitive ANTLR 4 Referece - Chapter 5: Designing Grammars (5.4 Dealing with Precedence, Left Recursion and Associativity), Chapter 6: Exploring Some Real Grammars
  3. Guido van Rossum, PEG Parsing Series Overview - A series of articles on parsing expression grammars
  4. ANTLR Website
  5. A collection of ANTLR4 grammars
comments powered by Disqus