◐
|  Edit
compsci typescript javascript

Gödel's System T in TypeScript

Recently, I’ve been reading Bove and Dybjer’s paper on “Dependent Types at Work” where Kurt Gödel’s System T is briefly described. It is a type system based on the Simply Typed Lambda Calculus and includes booleans and natural numbers. The unusual thing about it is that it allows us to perform only primitive recursion, which considerably limits the number of possible programs we can write but on the other hand it guarantees that these programs always terminate. This means that System T is not Turing complete as we can express only a subset of the total computable functions.

How come we only have primitive recursion?

In Untyped Lambda Calculus we can define fixed point combinators which allow us to simulate recursion. So if System T is based lambda calculus, how come we can’t have non-primitive recursion? The reason is - the type system. Let’s recall from the article “On Recursive Functions” - and the \(\omega\) combinator which applies a term to itself:

\[\omega := \lambda x.xx\]

However, here we’re dealing with types. What would the type of this term be? Let’s assume the second \(x\) in \(xx\) be of type \(\alpha\). That means the first \(x\) should also be of type \(\alpha\). Here we arrive at a contradiction because the first \(x\) is a function so it should have a type \(\alpha \to \beta\) for some \(\beta\). Both terms should have the same type, hence the contradiction. Every fixed point combinator involves some kind of self-application, therefore, it cannot be expressed in Simply Typed Lambda Calculus thus making our language less powerful but on the other hand - more predictable.

Building Blocks

System T includes predefined constants for True, False and Zero, as well as the Succ, Cases and Rec combinators, which represent the successor function, if-then-else, and primitive recursion respectively. Having this in our arsenal, we can now build some abstractions.
In the paper, the authors define the primitives and some operators in Agda and leave some additional tasks to the reader. So I tried to implement this system in TypeScript, which turned out to be a fun exercise.

Primitives

const Succ = (x: number): number => x + 1;

function Cases<T>(cond: boolean, a: T, b: T): T {
	return cond ? a : b;
}

It’s easy to see that Cases<number>(true, 1, 2) == 1 and Cases<number>(false, 1, 2) == 2.

function Rec<T>(sn: number, s: T, t: (z: number, acc: T) => T): T {
	return sn === Zero ? s : t(sn - 1, Rec(sn - 1, s, t));
}

It might seem confusing at first but its reduction is straightforward:

Rec 0 s t → s
Rec sn s t → t n (R n s t)

Rec<T> is a polymorphic function that takes three arguments (or four if we count the type). sn is the natural number on which we perform the recursion, think of sn as the successor of n. s is the element returned from the base case, whereas t is the function called on each recursive step. z enumerates each recursive step, and acc is the value which we “accumulate” over the recursion. Later in the examples, we’ll see that we can use Rec<T> as a higher order function too.

Arithmetic Operators

This is where it gets interesting. We construct the addition operator in the following way:

function add(x: number, y: number): number {
    return Rec<number>(x, y, (z, acc) => Succ(acc));
}

Seems weird? Let’s see what happens when we invoke add(2, 2):

t := λz.λacc.Succ acc

add 2 2 
→ Rec 2 2 t
→ t 1 (Rec 1 2 t)
→ t 1 (t 0 (Rec 0 2 t))
→ t 1 (t 0 2)
→ t 1 3
→ 4

Using it as a building block we can define multiplication:

function multiply(x: number, y: number): number {
    return Rec<number>(y, Zero, (z, acc) => add(x, acc));
}

As well as exponentiation:

function exp(x: number, y: number): number {
    return Rec<number>(y, 1, (z, acc) => multiply(x, acc));
}

We can also define the predecessor function:

function pred(x: number): number {
    return Rec<number>(x, Zero, (z, acc) => z);
}

This is a bit different than what we’ve been defining so far and it might not be so obvious why it works. t is a function that takes two arguments and returns the first one. Let’s walk through the reduction sequence of pred(3):

t := λz.λw.z

pred 3 
→ Rec 3 0 t
→ t 2 (Rec 2 0 t)
→ t 2 (t 1 (Rec 1 2 t))
→ t 2 (t 1 (t 0 (Rec 0 2 t)))
→ t 2 (t 1 (t 0 2))
→ t 2 (t 1 0)
→ t 2 1
→ 2

subtraction is very similar to addition, we just have to replace Succ with pred. You can check it out yourself.

Boolean Operators

Use the Cases<T> combinator with true and false constants to construct logical operators:

function not(x: boolean): boolean {
    return Cases<boolean>(x, false, true);
}

function and(x: boolean, y: boolean): boolean {
    return Cases<boolean>(x, y, false);
}

function or(x: boolean, y: boolean): boolean {
    return Cases<boolean>(x, true, y);
}

Based on this you can try implementing the xor operator.

Now it’s time to compare numbers. For that we’re going to reuse some of the functions we implemented so far and define to isZero: Nat → Bool. It uses the recursor, that is, if we’re in the base case (x equals Zero) we return True, otherwise False.

const isZero = (x: number): boolean => {
    return Rec<boolean>(x, true, (z, acc) => false);
}

function eq(x: number, y: number): boolean {
    return and(isZero(subtract(x, y)), isZero(subtract(y, x)));
}

function gt(x: number, y: number): boolean {
    return not(isZero(subtract(x, y)));
}

function lt(x: number, y: number): boolean {
    return not(isZero(subtract(y, x)));
}

Now reusing the operators above it is straightforward to define “greater than or equal to” ≥ and “less than or equal to” ≤.

Beyond Primitive Recursion

Now to our last and most interesting example. In System T we can express the total computable functions using primitive recursion, but can we express the ones that are not primitive recursive?

Ackermann

The Ackermann function is one of the earliest discovered examples of a total computable function that is not primitive recursive. All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive.

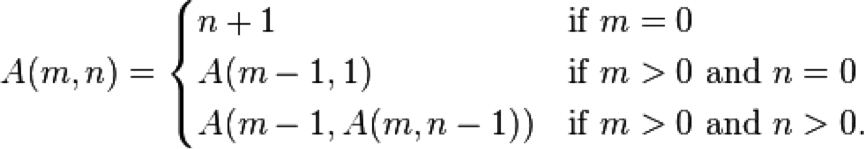
Ackermann Definition

You can find this neat visual example of its execution.

Let’s try to implement it within our type system! We’ll start by defining an operator for function composition:

type OneArityFn<T, K> = (x: T) => K;

function compose<T, K, V>(f: OneArityFn<K, V>, g: OneArityFn<T, K>)
    : OneArityFn<T, V> {
    return x => f(g(x));
}

Observe that compose is a higher order function. It takes two functions f and g and returns a new function that takes an input x, applies it to g and returns the result of g(x) applied to f. Now, using the Gödel’s recursor let’s define a repeater function:

function repeat<T>(f: OneArityFn<T, T>, n: number)
    : OneArityFn<T, T> {
    return Rec<OneArityFn<T, T>>(
        n,
        x => x,
        (z, acc) => compose(f, acc));
}

Simply put, given a function f and a number n, repeat will invoke f on its output n number of times. Think of it as composing it with itself n number of times. For example repeat(f, 3) will result in x => f(f(f(x))). This is all we need to define ackermann:

function ackermann(x: number): OneArityFn<number, number> {
    return Rec<OneArityFn<number, number>>(
        x,
        Succ,
        (z, acc) => y => repeat(acc, y)(acc(Succ(Zero))));
}

ackermann(1)(1); // => 3

Turns out ackermann is, in fact, a higher-order primitive recursive function, hence the partial application. We can see in its definition that we decrement the first argument on each step (which guarantees that it’ll terminate), and based on its value we compose a new execution branch which involves a seperate primitive recursor. The result is constructed via finite composition of the successor Succ function. Think of acc as an accumulated composition of the successor function.

Conclusion

Gödel’s System T has been influential in defining the Curry-Howard isomorphism or in other words - for establishing the relationship between computer programs and mathematical proofs. We can think of a type system as a set of axioms and type checkers as automatic theorem provers based on these axioms. We have seen that using a language with a particular type system always comes with its tradeoffs. Type systems with less expressive power reduce the number of possible programs we can write but on the other hand provide additional safety and potential performance benefits.

In some cases, a strongly typed language can be detrimental to our project’s long term success, in other cases, it might provide little to no additional value. That’s why when picking a language for a specific task, we have to carefully consider what’s going to best serve our needs.

Further Reading and References

comments powered by Disqus